6.5 Heat engine and refrigeration cycle

Problem Statement

Work produced in a heat engine is used to drive the compressor of a refrigration cycle as shown in the figure below. The heat source of the heat engine gains heat at \(T_{H@HE}=350^{\circ} C\) and the refrigration cycle is meant to absorb heat from a cold room at \(T_{L@Ref}=-10^{\circ} C\). Heat dissipation of both cycles happen ideally at the temperature same as environment as \(T_{L@HE}=T_{H@Ref}=25^{\circ} C\). Given both the cycles are operating at their most idael condition, for \(\dot Q_{L@Ref}=10\:kW\) of cooling required at the cold room, determine

a) how much heat is to be supplied at the heat source \(\dot Q_{H@HE}\) and

b) how much heat is dissipated to the environment .

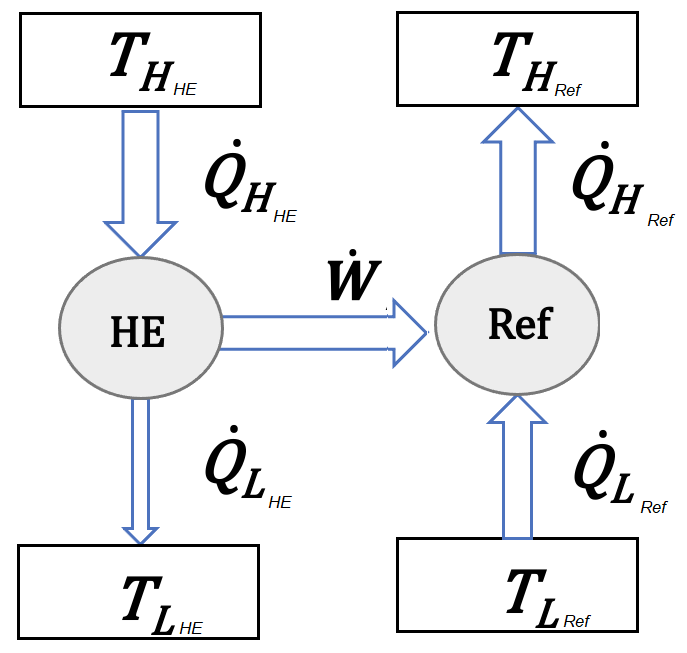
Solution Approach for a)

the most ideal case for the heat engine and the refrigration cycle happens when they operate as Carnot cycles. Therefore, fot the refrigration cycle

\(COP = \dot Q_{L@Ref}/\dot W=T_{L@Ref}/(T_{H@Ref}-T_{L@Ref})\)

and for the heat engine

\(\eta=\dot W/\dot Q_{H@HE}=1-T_{L@HE}/T_{H@HE}\)

therfore the work exchange between the refrigration cycle and the heat engine would be

\(\dot W=\dot Q_{L@Ref}/COP\)

and the heat input from the heat source

\(\dot Q_{H@HE}=\dot W/\eta\)

#define variables
import numpy as np

T_HHE = 350 + 273.15   #heat source temperature in K
T_LRef = -10 + 273.15   #cold room temperature in K
T_LHE = 25 + 273.15   #heat engine sink temperature in K
T_HRef = 25 + 273.15   #heat sink temperature for refrigration cycle in K
Q_LRef = 10E+3   #cooling load required in W

COP = T_LRef / (T_HRef - T_LRef)   #COP of the refrigration cycle
W = Q_LRef / COP   #work exchange in W

etha = 1 - T_LHE / T_HHE   #efficiency of the heat engine
Q_HHE = W / etha   #heat received from heat source in W

Q_HHE
print('The amount of heat required is:', f"{Q_HHE/1000:.1f}", 'kW')

The amount of heat required is: 2.6 kW

Solution Approach for b)

looking at the system as a whole, based on the first law

\(\dot Q_{in} = \dot Q_{out}\)

\(\dot Q_{H@HE}+\dot Q_{L@Ref}=\dot Q_{L@HE}+\dot Q_{H@Ref}\)

and the total heat dissipated to the environment is

\(\dot Q_L=\dot Q_{L@HE}+\dot Q_{H@Ref}\)

therefore

\(\dot Q_L=\dot Q_{H@HE}+\dot Q_{L@Ref}\)

Q_L = Q_LRef + Q_HHE   #total heat dissipation

print('The total amount of heat dissipated to the environment is:', f"{Q_L/1000:.1f}", 'kW')

The total amount of heat dissipated to the environment is: 12.6 kW