Ctrl+K

Chapter 6

Chapter 6#

Question #17: Geothermal Heat Pump#

The following list is the average weekly temperature history for the three months (12 weeks) of winter (Dec, Jan, Feb) in Whistler, Canada. Consider a room in this weather that is maintained at \(T_r=21\:^{\circ}C\)

\(T(^{\circ}C)=[-1, -3, -2, -3, -2, -4, -5, -2, -5, -4, -1, 0]\)

a) plot the weekly temperature history

b) calculate and plot the Carnot COP for a heat pump operating between the room temperature and the weekly reported temperature in Whistler.

Now consider using a geothermal heat pump where the evaporator of the cycle is placed deep into the soil where the temperature is almost constant year-round at \(T_s=3\:^{\circ}C\).

c) calculate the Carnot COP for a geothermal heat pump operating in this condition

Solution Approach for a)#

#import libraries
import numpy as np
import matplotlib.pyplot as plt

#define variables
T = np.array([-1,-3,-2,-3,-2,-4,-5,-2,-5,-4,-1,0])
weeks = np.arange(1,13)

plt.plot(weeks,T, marker=4 ,linestyle='None')
plt.ylabel("Temperature [C]")  # give y axis a label
plt.xlabel("Weeks")  # give x axis a label

Text(0.5, 0, 'Weeks')
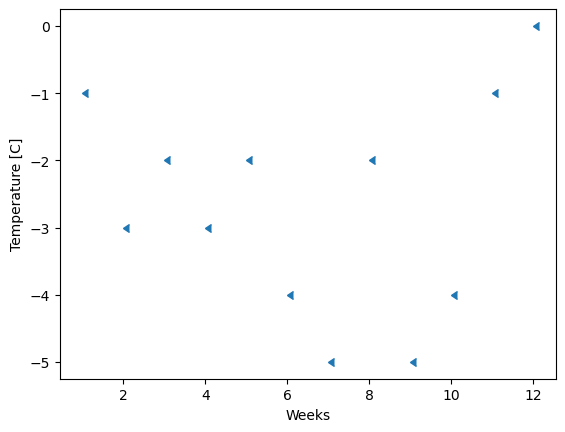
../../_images/9a3c0ee0539b235374f3bc0adb780cc3edc3d5e94f9accfe3e1bc2395523f2a5.png

Solution Approach for b)#

for a Carnot heat pump

\(COP_{Carnot}=T_H/(T_H-T_C)\)

#define variables
T_r = 21 + 273.15   #room temperature in K
T_H = T_r   #room as the hot heat sink
T_C = T + 273.15   #outside temperature as the cold heat source in K

COP_b = T_H / (T_H - T_C)   #Carnot COP based on outside temperature

plt.plot(weeks,COP_b,marker=4 ,linestyle='None')
plt.ylabel("COP")  # give y axis a label
plt.xlabel("Weeks")  # give x axis a label

Text(0.5, 0, 'Weeks')
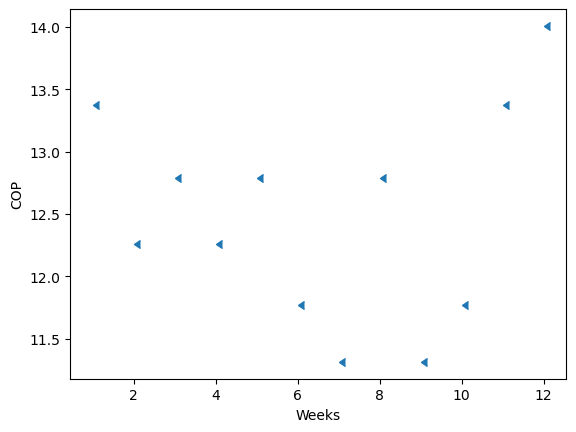
../../_images/51213e87f14a7339ef1f7a5262e64f8f8253ad5a5ebc02b38ecc69dcbd0384be.png

Solution Approach for c)#

T_C = 3 + 273.15   #cold heat source temperature in K

COP_c = T_H / (T_H - T_C)   #Carnot COP based on geothermal heat pump 

print('The Carnot COP of a geothermal heat pump in this condition is:', f"{COP_c:.1f}")

The Carnot COP of a geothermal heat pump in this condition is: 16.3
Contents