6.3 Rankine Cycle#
Problem Statement#
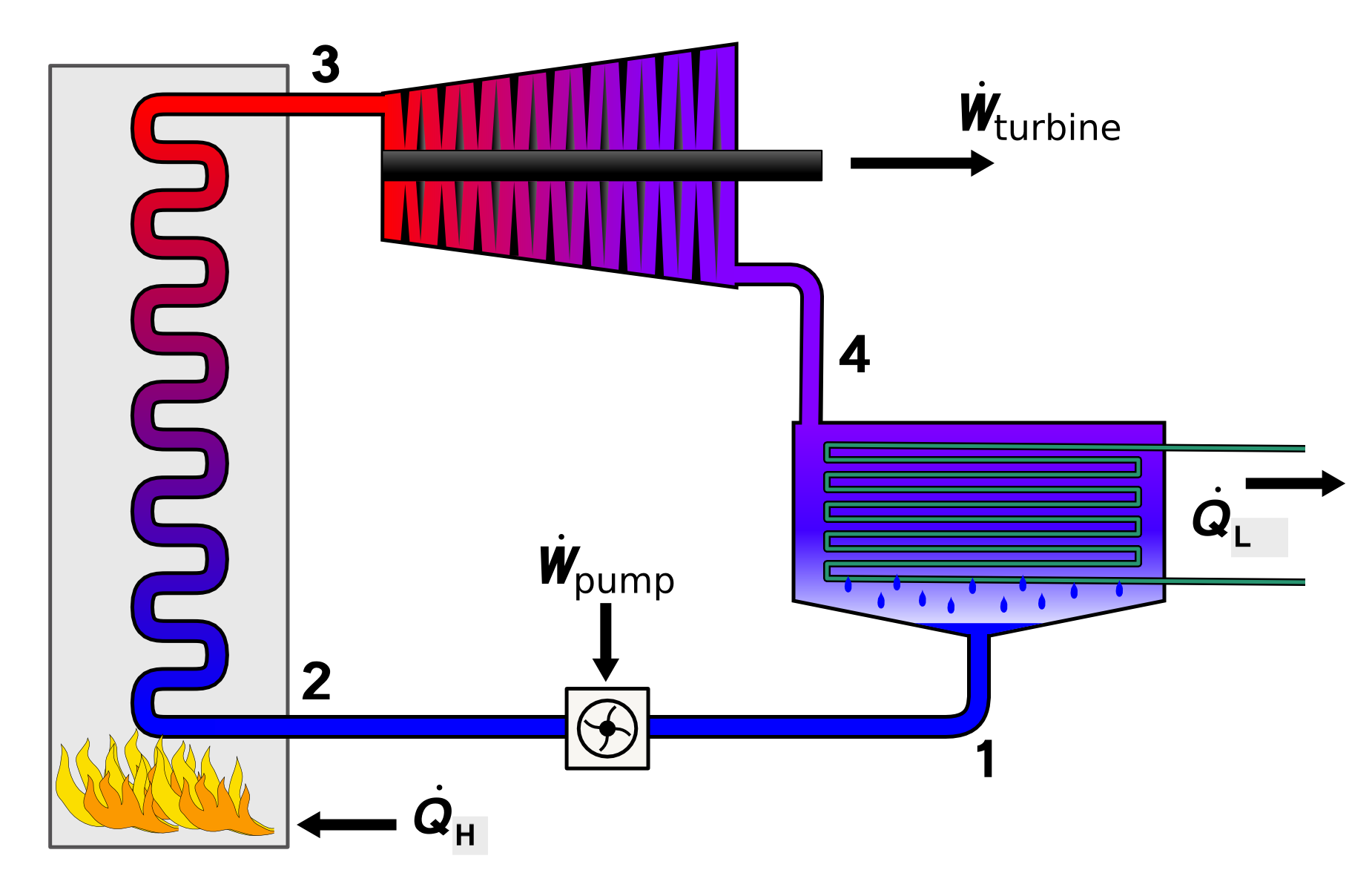
Consider a heat engine in the form of a rankine cycle shown in the figure below. The cycle’s heat input is \(\dot Q_H=50\:MW\) through a bolier at \(T_H=500^{\circ} C\), and the cycle dissipates \(\dot Q_L=30\:MW\) of heat to the environment through a condenser at \(T_L=30^{\circ} C\).
a) calculate the efficiency of the engine
b) how ideal the system is compared to its Carnot efficiency
c) an idea is proposed to increase the boiler temperature by \(50^{\circ} C\) up to \(T_H=550^{\circ} C\). How would this potentially impact the efficiency.
d) the piping system in the condenser gets rusty over-time causing restricted coolant flow and consequently increased heat sink temperature to \(T_L=35^{\circ} C\). How would the affected flow potentially impact the efficiency.
e) seasonal changes in temperature causes the operating temperatures of both the heat sink and the heat source to drop by \(50^{\circ} C\) to \(T_H=450^{\circ} C\) and \(T_L=-20^{\circ} C\). How would seasonal changes potentially impact the efficiency.
Solution Approach for a)#
\(\eta=\dot W/\dot Q_H=1-\dot Q_L/\dot Q_H\)
# define variables
Q_H = 50E+6 #cycle heat input in W
Q_L = 30E+6 #cycle heat dissipation in W
T_H = 500 + 273.15 #heat source temperature in K
T_L = 30 + 273.15 #heat sink temperature in K
etha = 1 - Q_L / Q_H #the efficiency
print('The efficiency of the cycle is:', f"{etha * 100:.1f}", '%')
The efficiency of the cycle is: 40.0 %
Solution Approach for b)#
to evaluate the carnot efficiency
\(\eta_{Carnot}=1-T_L/T_H\)
etha_c = 1 - T_L / T_H
print('The Carnot efficiency of the cycle is:', f"{etha_c * 100:.1f}", '%')
The Carnot efficiency of the cycle is: 60.8 %
Solution Approach for c)#
Carnot efficiency is a tool to have a ballpark estimation if how changes in heat source/sink temperatures will likely impact efficiency.
T_H_m = 550 + 273.15 #modified heat source temperature in K
etha_c = 1 - T_L / T_H_m
print('The Carnot efficiency after increasing boiler temperature is:', f"{etha_c * 100:.1f}", '%')
The Carnot efficiency after increasing boiler temperature is: 63.2 %
Solution Approach for d)#
T_L_m = 35 + 273.15 #modified heat sink temperature in K
etha_c = 1 - T_L_m / T_H
print('The Carnot efficiency under restricted condenser flow is:', f"{etha_c * 100:.1f}", '%')
The Carnot efficiency under restricted condenser flow is: 60.1 %
Solution Approach for e)#
T_H_m = 450 + 273.15 #modified heat source temperature in K
T_L_m = -20 + 273.15 #modified heat sink temperature in K
etha_c = 1 - T_L_m / T_H_m
print('The Carnot efficiency under seasonal temperature drop is:', f"{etha_c * 100:.1f}", '%')
The Carnot efficiency under seasonal temperature drop is: 65.0 %
