Ctrl+K

6.16 Multilevel Carnot Heat Engine

6.16 Multilevel Carnot Heat Engine#

Problem Statement#

Consider a two-level heat engine working between a heat source (\(\dot Q_H=100\:kW\)) at \(T_H=400^\circ C\) and a heat sink at \(T_L=0^\circ C\). The heat rejected from the first level (\(HE_1\)) is used as input to the second level (\(HE_2\)). The heat transfer between two levels (\(\dot Q_M\)) happens at a medium temperature (\(T_M\)).

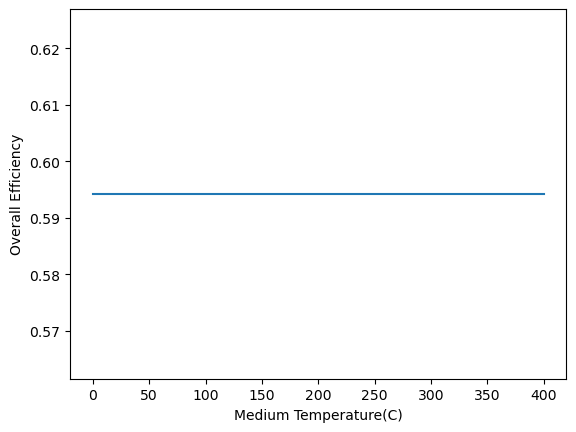
a) Plot the efficiency of the system based on the medium temperature (\(T_M\)) assuming Carnot cycles for both the heat engines. How is the trend?

b) Try proving mathematically

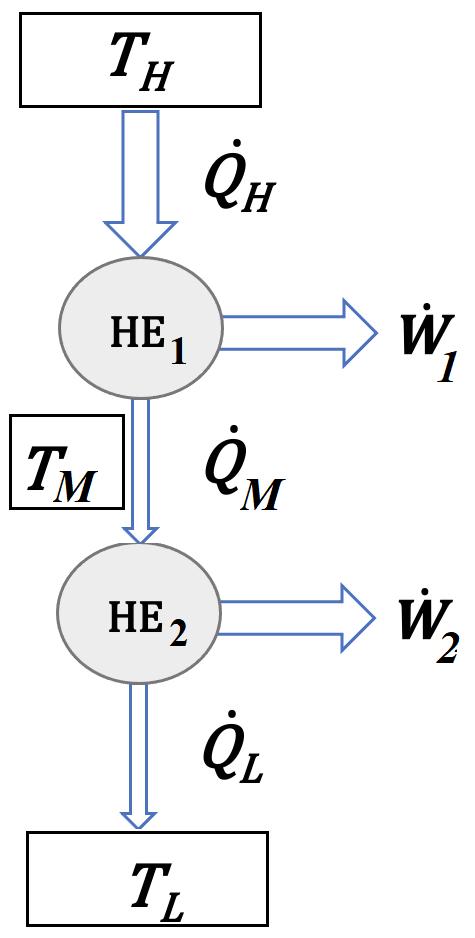
CH6-Q15.png

Solution Approach for a)#

for a Carnot cycle,

\(\eta_{Carnot}=1-T_M/T_H=\dot W_1/\dot Q_H\)

and from the first law

\(\dot Q_H=\dot Q_M+\dot W_1\)

the same principle applies for the heat engine working at lower temperatures

#import the libraries we'll need
import numpy as np
import matplotlib.pyplot as plt

Q_H = 100   #heat input in kW
T_H = 400 + 273.15   #heat source temperature in K
T_L = 0 + 273.15   #heat sink temperature in K

T_M = np.linspace(T_L, T_H, 1000)  # define an array of values for the medium temperature (T_M)

etha_1 = 1 - T_M / T_H   #efficiency values for heat engine #1
W_1 = etha_1 * Q_H   #work values for heat engine #1 in kW
Q_M = Q_H - W_1   #heat exchange between heat engines is kW

etha_2 = 1 - T_L / T_M   #efficiency values for heat engine #2
W_2 = etha_2 * Q_M   #work values for heat engine #1 in kW

etha = (W_1 + W_2) / Q_H   #overall efficiency

T_M_C = T_M - 273.15   #medium temperature in C
plt.plot(T_M_C, etha)

plt.ylabel("Overall Efficiency")  # give y axis a label
plt.xlabel("Medium Temperature(C)")  # give x axis a label

Text(0.5, 0, 'Medium Temperature(C)')
../../_images/944545eb9e1106df635d74c8ea6f240fbd663d0fca6ab3d493f6ba4ee994b5ca.png

Solution Approach for b)#

The overall efficiency of the system is based on heat input and total work

\(\eta=\dot W/\dot Q_H=(\dot W_1+\dot W_2)/\dot Q_H\)

for heat engine (1)

\(\eta_1=\dot W_1/\dot Q_H=\eta_{Carnot}=1-T_M/T_H\)

therefore

\(\dot W_1=\dot Q_H(1-T_M/T_H)\)

for heat engine (2)

\(\eta_2=\dot W_2/\dot Q_M=\eta_{Carnot}=1-T_L/T_M\)

therefore

\(\dot W_2=\dot Q_M(1-T_L/T_M)\)

from the first law for heat engine (1)

\(\dot Q_H=\dot Q_M+\dot W_1\)

so

\(\dot Q_M=\dot Q_H-\dot W_1=\dot Q_H-\dot Q_H(1-T_M/T_H)=\dot Q_H(T_M/T_H)\)

substituting into the equation for \(\dot W_2\)

\(\dot W_2=\dot Q_H(T_M/T_H)(1-T_L/T_M)=\dot Q_H(T_M-T_L)/T_H\)

substituting into the equation for \(\eta\)

\(\eta=(1-T_M/T_H)+(T_M-T_L)/T_H=1-T_L/T_H\)

which is independent of the medium temperature

Contents