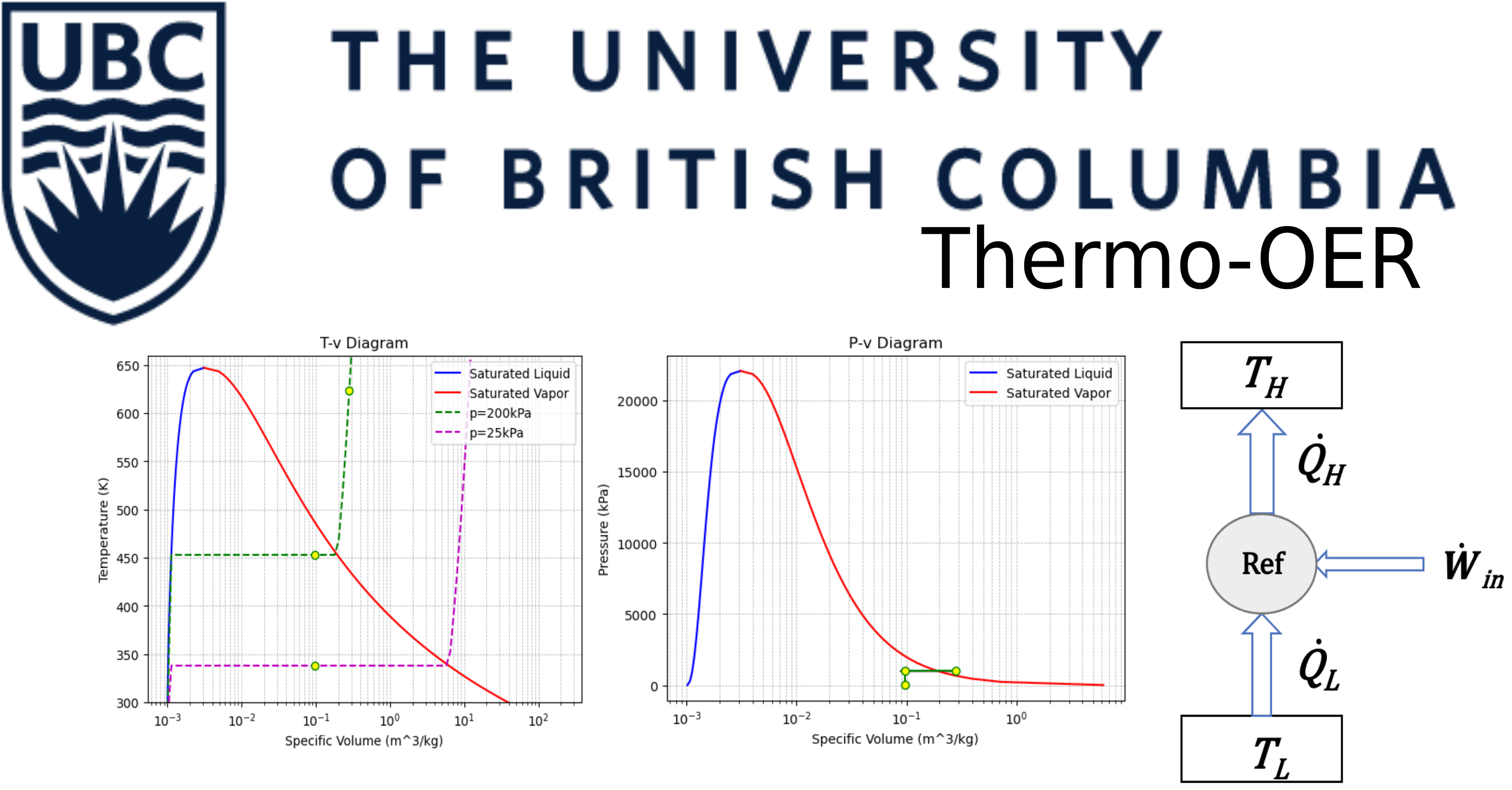
2.7: Weighted Piston and Pressed Spring#
A cyliner and piston system is equipped with an spring with a constant of \(k=200\:kN/m\) to keep air pressurized at \(P=2\:atm\). Consodering the atmospheric pressure around the system is \(P_a=1\:atm\) and the piston weighs \(m=1\:kg\) in mass and has a diameter of \(D=25\:cm\), calculate
a) pressure contribution from the piston
b) pressure contribution from the spring
c) how lond the spring is to be compressed in order to reach the desired pressure.
Solution Approach for a)#
The pressure enforced by the piston comes from its mass where
\(F=mg\)
where \(m\) is the piston mass and \(g\) is the gravitationalacceleration. and,
\(P_p=F/A\)
where \(A\) is the piston surface area
#import libraries and define variables
import numpy as np
m = 1 #piston mass in kg
g = 9.8 #gravitational acceleration in m/s2
D = 0.25 #piston diameter in m
F = m * g #gravitational force on the piston
A = np.pi * D **2 / 4 #piston surface area in m2
P_p = F / A #piston pressure contribution in Pa
print('The pressure conttribution from the piston is:', f"{P_p:.1f}", 'Pa')
The pressure conttribution from the piston is: 199.6 Pa
Solution Approach for b)#
The pressure of air inside the system is a sum of atmospheric pressure (\(P_a\)), the pressure enforced by the piston mass (\(P_p\)), and the pressure enfored by the spring force (\(P_s\)). Therefore,
\(P=P_a+P_p+P_s\)
and
\(P_s=P-P_a-P_p\)
#define variables
P_a = 101325 #atmospheric pressure in Pa
P = 2 * P_a #air pressure inside the system in Pa
P_s = P - P_a - P_p
print('The pressure conttribution from the spring is:', f"{P_s:.1f}", 'Pa')
The pressure conttribution from the spring is: 101125.4 Pa
Solution Approach for c)#
The pressure enforced by the sping comes fom the force enforced by its being compressed over the surface area of the piston
\(P_s=F_s/A\)
therefore
\(F_s=P_s\times A\)
and \(F_s=k\Delta x\)
where \(x\) is the length of spring compression from neutral
therfore
\(\Delta x=F_s/k=(P_s\times A)/k\)
#define variables
k = 200E+3 #spring constant in N/m
x = P_s * A / k #spring deformation in m
print('The spring is compressed', f"{x*100:.1f}", 'cm to in order for air to reach the desired pressure')
The spring is compressed 2.5 cm to in order for air to reach the desired pressure