6.4 Refrigeration/ heat pump system#
Problem Statement:#
Consider a refrigration/heat pump system with a work input of \(\dot W_{in}=2\:kW\) delivering \(\dot Q_L=5\:kW\) of heat from a cold environment at \(T_L=-10^{\circ} C\) and releasing heat to a hot environment at \(T_H=50^{\circ} C\).
a) calculate the heat released into the hot environment based on the first law
b) calculate the COP of the cycle based on 1) refrigration and 2) heat pump
c) evaluate how well the cycle works compared to its Carnot equivalent
d) assuming the cycle as a heat pump, the hot environment temperature is required to increase by \(5^{\circ} C\) to provide more heating power to the room during peak days of winter. How would this potentially impact COP.
e) assuming the cycle as a refrigration system, the temperature in the cold environment is required to increase by \(5^{\circ} C\) to prevent frosting in the evaporator. How would this potentially impact COP.
f) due to seasonal temperature variations, the operating temperature of both the hot and cold environments drop by \(5^{\circ} C\) in the cold season. How would this impact the COP given the cycle is a 1) refrigration system 2) heat pump
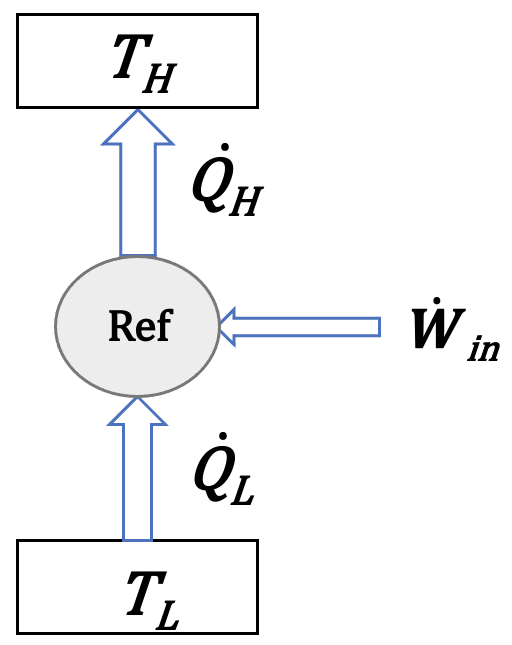
Solution Approach for a)#
based on the first law,
\(\dot Q_H=\dot Q_L+\dot W_{in}\)
W_in = 2e+3 #work input in W
Q_L = 5e+3 #heat absorbed from the cold environment in W
T_L = -10 + 273.15 #cold environment temperature in K
T_H = 50 + 273.15 #hot environment temperature in K
Q_H = Q_L + W_in #heat released into the hot environment in W
print('The amount of heat released into the hot environment is:', f"{Q_H/1000:.1f}", 'kW')
The amount of heat released into the hot environment is: 7.0 kW
Solution Approach for b)#
for a refrigration cycle,
\(COP_R=\dot Q_L/\dot W_{in}\)
and for a heat pump
\(COP_H=\dot Q_H/\dot W_{in}\)
COP_R = Q_L / W_in # COP of refrigration
COP_H = Q_H / W_in # COP of heat pump
print('The COP for the refrigration cycle is:', f"{COP_R:.1f}")
print('The COP for the heat pump cycle is:', f"{COP_H:.1f}")
The COP for the refrigration cycle is: 2.5
The COP for the heat pump cycle is: 3.5
Solution Approach for c)#
based on 6.4.3,
\(COP_{RC} = T_L/(T_H-T_L)\)
\(COP_{HC} = T_H/(T_H-T_L)\)
COP_RC = T_L / (T_H - T_L) #Carnot COP of refrigration
COP_HC = T_H / (T_H - T_L) #Carnot COP of heat pump
print('The Carnot COP for the refrigration cycle is:', f"{COP_RC:.1f}")
print('The Carnot COP for the heat pump cycle is:', f"{COP_HC:.1f}")
The Carnot COP for the refrigration cycle is: 4.4
The Carnot COP for the heat pump cycle is: 5.4
Solution Approach for d)#
the Carnot COP is a reasonable estimation to get an idea of how changes in temperature would potentially impact COP
T_H_m = T_H + 5 #adjasted hot environment temperature in K
COP_HCm = T_H_m / (T_H_m - T_L) #Carnot COP of heat pump for the adjusted temperature
print('The Carnot COP for the heat pump cycle with adjusted temperature is:', f"{COP_HCm:.1f}")
The Carnot COP for the heat pump cycle with adjusted temperature is: 5.0
Solution Approach for e)#
T_L_m = T_L + 5 #adjasted cold environment temperature in K
COP_RCm = T_L_m / (T_H - T_L_m) #Carnot COP of refrigration system for the adjusted temperature
print('The Carnot COP for the refrigration cycle with adjusted temperature is:', f"{COP_RCm:.1f}")
The Carnot COP for the refrigration cycle with adjusted temperature is: 4.9
Solution Approach for f)#
T_H_m = T_H - 5 #dropped hot environment temperature in K
T_L_m = T_L - 5 #dropped cold environment temperature in K
COP_HCm = T_H_m / (T_H_m - T_L_m) #Carnot COP of heat pump for the dropped temperature
COP_RCm = T_L_m / (T_H_m - T_L_m) #Carnot COP of refrigration system for the dropped temperature
print('The Carnot COP for the refrigration cycle with dropped seasonal temperature is:', f"{COP_RCm:.1f}")
print('The Carnot COP for the heat pump cycle with dropped seasonal temperature is:', f"{COP_HCm:.1f}")
The Carnot COP for the refrigration cycle with dropped seasonal temperature is: 4.3
The Carnot COP for the heat pump cycle with dropped seasonal temperature is: 5.3
