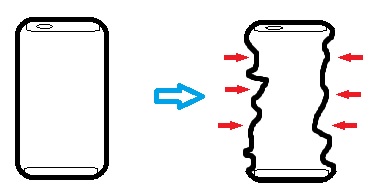
3.9: Can Crush

Consider a Can Crush experiment where an empty can is crushed using the pressure drop caused by instant cooling of the hot air trapped inside the can. An empty \(355\:ml\) can at atmospheric pressure is heated up to \(T=120^{\circ} C\) on a stove. Then can is then suddenly dipped upside-down into a bowl of water at \(T_w=25^{\circ} C\). Assumming the air inside the can is ideal gas in thermal equilibrium with the can, calculate:

a) mass of heated air inside the can

b) the crushing temperature for air inside the can assuming a pressure difference on \(P_c=20\:kPa\) is required to commence crushing

Solution Approach for a)

based on ideal gas assumption,

\(PV=mRT\)

so

\(m=PV/(RT)\)

#define variables
P_a = 101325   #atmospheric pressure in Pa
R = 287   #gas constant in J/kg.K

T = 120 + 273.15   #temperature in K
P = P_a   #initial hot air pressure in Pa
V = 355E-6   #gas container volume in m3

m = P * V / (R * T)   #mass in kg

print('The amount of hot air stored in the can is:', f"{m*1000:.3f}", 'mg')

The amount of hot air stored in the can is: 0.319 mg

Solution Approach for b)

The pressure difference (\(P_c\)) is the differece between the atmospheric pressure outside the can (\(P_a\)) and the pressure inside the can (\(P\))

\(P_c=P_a-P\)

so

\(P=P_a-P_c\)

then assuming idael gas for the air inside the can at this pressure

\(T=PV/(mR)\)

note the volume of the can is constant before the crush happens

P_c = 20E+3   #pressure difference in Pa

P = P_a - P_c
T = P * V / (m * R)   #crushing temperature in K

print('The crushing temperature based on the pressure difference is:', f"{T-273.15:.1f}", 'C')

The crushing temperature based on the pressure difference is: 42.4 C