6.15 Detailed Entropy Generation for a Steam Cycle#
Problem Statement:#
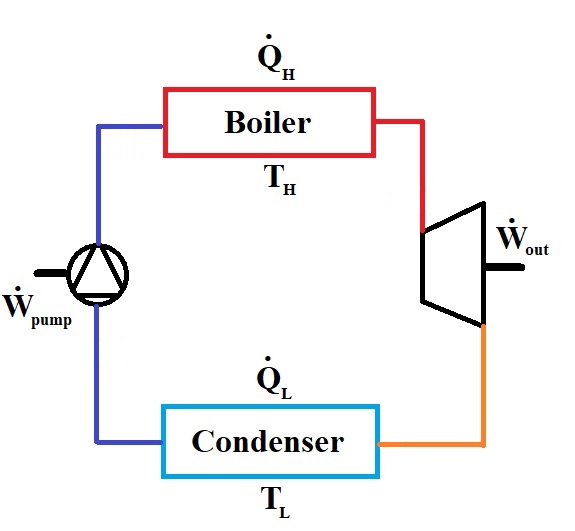
Consider a steam turbine cycle as shown in the figure below. \(\dot m=1\:kg/s\) of water enters the pump as saturated liquid at \(P_1=101\:kPa\) and is pressurized to \(P_2=1\:MPa\) before entering the boiler. Water is then heated in the bioler in constant pressure till its temperature reached \(T_3=600\:^{\circ}C\). The steam is then used in a turbine to produce work until it reaches to temperature of \(T_4=260\:^{\circ}C\). The steam is then cooled in a constant-pressure condenser to reach its saturated liquid state before entering the pump. Assuming the boiler to be a heat source at \(T_H=650\:^{\circ}C\) and the condenser to be a heat sink at \(T_L=20\:^{\circ}C\), calculate:
a) the pump work assuming the dinsity of water remain constant through pumping
b) amount of heat supplied in the boiler
c) amount of work output in turbine
d) amount of heat dissipated in the condenser based on inlet and outlet enthalpies
e) amount of heat dissipated in the condenser looking to the system as a whole
f) entropy generation in the pump
g) entropy generation in the boiler
h) entropy generation in the turbine
i) entropy generation in the condenser
j) total entropy generation based on entropy generation for each element
k) total entropy generation considering the cycle as a heat engine
Solution Approach for a)#
state (1) is a satuated liquid at \(P_1=101\:kPa\) and state (2) is pressurized water with the same density as in state (1)
from the first law for the pump
\(\dot W_P=\dot m(h_2-h_1)\)
import CoolProp.CoolProp as CP
fluid = "water" # define the fluid or material of interest
P_1 = 101E+3 #pressure in state (1) in Pa
P_2 = 1E+6 #pressure in state (2) in Pa
m = 1 #water flow-rate in kg/s
h_1 = CP.PropsSI("H", "P", P_1, "Q", 0 , fluid) #enthalpy in state (1) in J/kg
d_1 = CP.PropsSI("D", "P", P_1, "Q", 0 , fluid) #density in state (1) in kg/m3
d_2 = d_1 #density in state (2) in kg/m3
h_2 = CP.PropsSI("H", "P", P_2, "D", d_2 , fluid) #enthalpy in state (2) in J/kg
W_P = m * (h_2 - h_1)
print('The pump work for the cycle is:', f"{W_P/1000:.1f}", 'kW')
The pump work for the cycle is: 3.1 kW
Solution Approach for b)#
The boiler is assumed in a constant pressure, so
\(P_3 = P_2\)
and from the first law for the boiler
\(\dot Q_H=\dot m(h_3-h_2)\)
#define variables
P_3 = P_2 #pressure of state (3) in Pa
T_3 = 600 + 273.15 #temperature of state (3) in K
h_3 = CP.PropsSI("H", "P", P_3, "T", T_3 , fluid) #enthalpy in state (3) in J/kg
Q_H = m * (h_3 - h_2)
print('The amount of heat supplied in boiler is:', f"{Q_H/1000:.1f}", 'kW')
The amount of heat supplied in boiler is: 3276.8 kW
Solution Approach for c)#
The condenser is assumed to operate in a constant pressure
\(P_4=P_1\)
and from the first law
\(\dot W=\dot m(h_3-h_4)\)
P_4 = P_1 #pressure in state (4) in Pa
T_4 = 260 + 273.15 #temperatue in state (4) in K
h_4 = CP.PropsSI("H", "P", P_4, "T", T_4 , fluid) #enthalpy in state (4) in J/kg
W = m * (h_3 - h_4)
print('The amount of work output from the turbine is:', f"{W/1000:.1f}", 'kW')
The amount of work output from the turbine is: 704.2 kW
Solution Approach for d)#
first law for the condenser
\(\dot Q_L=\dot m(h_4-h_1)\)
Q_L = m * (h_4 - h_1)
print('The amount of heat dissipated in the condenser based on inlet/outlet enthalpies is:', f"{Q_L/1000:.1f}", 'kW')
The amount of heat dissipated in the condenser based on inlet/outlet enthalpies is: 2575.7 kW
Solution Approach for e)#
The firts law for the whole system
\(E_in=E_out\)
\(\dot Q_H+\dot W_{pump}=\dot Q_L+\dot W\)
therefore
\(\dot Q_L=\dot Q_H+\dot W_{pump}-\dot W\)
Q_L = Q_H + W_P - W
print('The amount of heat dissipated in the condenser based the first law for the whole system is:', f"{Q_L/1000:.1f}", 'kW')
The amount of heat dissipated in the condenser based the first law for the whole system is: 2575.7 kW
Solution Approach for f)#
for an open steady-state system
\(\Sigma \dot m_es_e-\Sigma \dot m_is_i=\Sigma \dot Q/T+\dot S_{gen}\)
for the pump
\(\dot Q=0\)
therefore
\(S_{gen}=\dot m(s_2-s_1)\)
s_1 = CP.PropsSI("S", "P", P_1, "Q", 0 , fluid) #entropy in state (1) in J/kgK
s_2 = CP.PropsSI("S", "P", P_2, "D", d_2 , fluid) #entropy in state (2) in J/kgK
S_gen_P = m * (s_2 - s_1)
print('The amount of entropy generation in the pump is:', f"{S_gen_P:.1f}", 'W/K')
The amount of entropy generation in the pump is: 5.9 W/K
Solution Approach for g)#
for the boiler
\(\dot Q=\dot Q_H\)
therefore
\(S_{gen}=\dot m(s_3-s_2)-\dot Q_H/T_H\)
#define variables
T_H = 650 + 273.15 #heat source in boiler temperature in K
s_3 = CP.PropsSI("S", "P", P_3, "T", T_3 , fluid) #entropy in state (3) in J/kgK
S_gen_B = m * (s_3 - s_2) - Q_H / T_H
print('The amount of entropy generation in the boiler is:', f"{S_gen_B:.1f}", 'W/K')
The amount of entropy generation in the boiler is: 3169.7 W/K
Solution Approach for h)#
for the turbine
\(\dot Q=0\)
therefore
\(S_{gen}=\dot m(s_4-s_3)\)
s_4 = CP.PropsSI("S", "P", P_4, "T", T_4 , fluid) #entropy in state (4) in J/kgK
S_gen_T = m * (s_4 - s_3)
print('The amount of entropy generation in the turbine is:', f"{S_gen_T:.1f}", 'W/K')
The amount of entropy generation in the turbine is: 36.6 W/K
Solution Approach for i)#
for the condenser
\(\dot Q=\dot Q_L\)
therefore
\(S_{gen}=\dot m(s_1-s_4)+\dot Q_L/T_L\)
#define variables
T_L = 20 + 273.15 #heat sink temperature in K
S_gen_C = m * (s_1 - s_4) + Q_L / T_L
print('The amount of entropy generation in the condenser is:', f"{S_gen_C:.1f}", 'W/K')
The amount of entropy generation in the condenser is: 2024.6 W/K
Solution Approach for j)#
\(S_{gen}=S_{gen,pump}+S_{gen,boiler}+S_{gen,turbine}+S_{gen,condenser}\)
S_gen = S_gen_P + S_gen_B + S_gen_T + S_gen_C
print('The total entropy generation based on each element is:', f"{S_gen:.1f}", 'W/K')
The total entropy generation based on each element is: 5236.8 W/K
Solution Approach for k)#
from the second law for a closed system
\(S_{gen}=-\Sigma Q/T=-(Q_H/T_H-Q_L/T_L)\)
S_gen = - (Q_H / T_H - Q_L / T_L)
print('The total entropy generation looking at the system as a heat engine is:', f"{S_gen:.1f}", 'W/K')
The total entropy generation looking at the system as a heat engine is: 5236.8 W/K
