5.6 Refrigeration cycle: R134a#
Consider a refrigeration cycle working with R134-a as coolant to support \(100\:kW\) of cooling load to a cold storage. The refrigerant absorbs heat at \(-20^{\circ} C\) during evaporation and enters the compressor as saturated vapor. The compressor is coupled to a gas turbine working with compressed air that pressurizes R134-a increasing the coolant’s temperature to \(120^{\circ} C\). The refrigerant is then cooled down to saturated liquid at \(40^{\circ} C\) in a condensor in constant pressure before entering a throttling valve. The refrigerant is then throttled to \(-20^{\circ} C\) to provide refrigerating fluid for the evaporator. Given the turbine works with compressed air at \(1\:MPa\) gauge pressure and room temperature, determine the air flow-rate required to provide the required cooling load given the air is discharged to the atmosphere at the turbine outlet and goes through a polytropic process with \(n=1.5\).
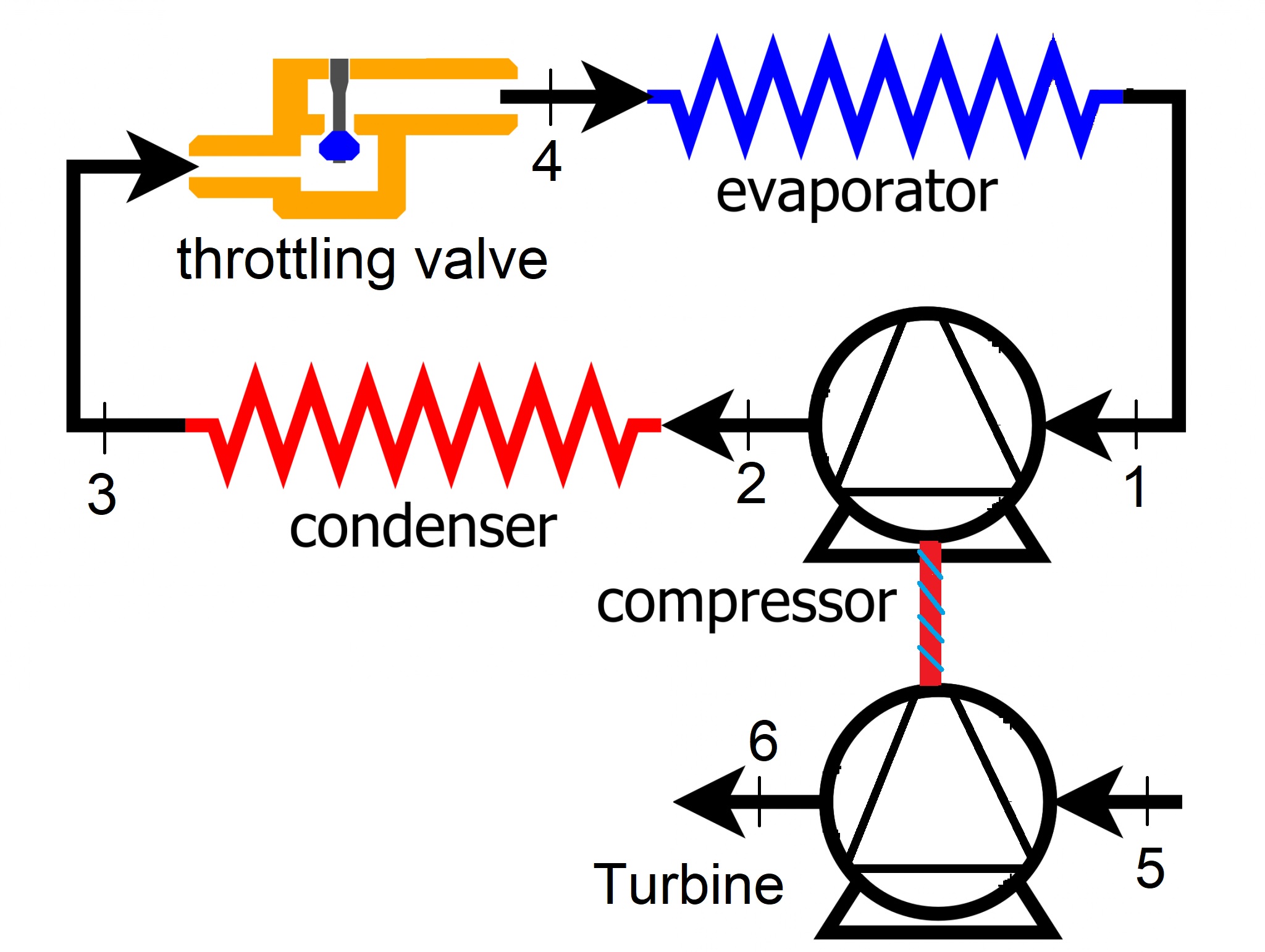
Solution Approach#
The enthalpy change through the evaporator per kg of the refrigerant is to be calculated. Afterwards, the flow-rate of refrigerant is calculated based on the cooling load, followed by calculation of compressor load based on flow-rate and work calculated per kg of refrigerant. From Q5 of this chapter:
# import the libraries we'll need
import CoolProp.CoolProp as CP
# define variables
fluid = "R134A" # define the fluid or material of interest
T_3 = 40 + 273.15 #state #3 temperature in K
h_3 = CP.PropsSI("H", "T", T_3, "Q", 0, fluid)/1000 # enthalpy of the refrigerant at state #3 in kJ/kg
h_4 = h_3 #constant enthalpy through a throttling valve
T_4 = -20 + 273.15 #temperature of refrigerant at state #4 in K
P_4 = CP.PropsSI("P", "T", T_4, "Q", 1, fluid) # pressure of the refrigerant at state #1 in Pa (quality is set to 1 as the pressure keeps constant in sat region)
T_1 = T_4 #temperature at state #1 in K
h_1 = CP.PropsSI("H", "T", T_1, "Q", 1, fluid)/1000 # enthalpy of the refrigerant at state #1 in kJ/kg
T_2 = 120 + 273.15 #temperature at state #2 in K
P_3 = CP.PropsSI("P", "T", T_3, "Q", 0, fluid) # pressure of the refrigerant at state #3 in Pa
P_2 = P_3 # pressure of the refrigerant at state #2 in Pa
h_2 = CP.PropsSI("H", "T", T_2, "P", P_2, fluid)/1000 # enthalpy of the refrigerant at state #2 in kJ/kg
q_c = h_1 - h_4
q_h = h_2 - h_3
w = h_2 - h_1
The total cooling load \(\dot Q_c\) is given to be \(100\:kW\); therefore the refrigerant flow-rate is calculated as
\(\dot m_{R134a}=\dot Q_c/q_c\)
Q_c = 100 #cooling load in kW
m_r134a = Q_c / q_c #refrigerant flow-rate in kg/s
The total work done by the compressor then would be,
\(\dot W_{R134a}=\dot m_{R134a}\:w\)
W_r134a = m_r134a * w #the work input by the compressor in kW
Now, looking at the turbine-compressor coupling, the work required by the compressor is supported by the turbine in which air goes through a polytropic process. For a polytropic process,
\(Pv^n=constant\)
\(P_1v_1^k=P_2v_2^k\)
\(d (density)=1/v\)
\(d_2/d_1=(P_2/P_1)^{(1/k)}\)
\(d_2=d_1\:(P_2/P_1)^{(1/k)}\)
#thermodynamic properties and constants for air at state #5
fluid = "Air"
R = 0.287 #air gas constant in kJ/kg.k
P_atm = 101.325 #atmospheric pressure in kPa
P_gauge = 1000 #guage presssure at turbine inlet in kPa
P_5 = P_gauge + P_atm
T_5 = 25 + 273.15 #compressed air temperature in K
D_5 = CP.PropsSI("D", "T", T_5, "P", P_5, fluid) #air density at turbine inlet
P_6 = P_atm #pressure at turbine outlet in kPa
n = 1.5
D_6 = D_5 * (P_6/P_5) ** (1/n)
Now, considering the first law of thermodynamics,
\(w_{turbine} = h_5 - h_6\)
\(\dot W_{turbine}=\dot m_{air} \:(h_5-h_6)\)
and from the coupling
\(\dot W_{turbine}=\dot W_{R134a}\)
\(\dot m_{air}=\dot W_{R134a}/(h_5-h_6)\)
fluid = "Air"
h_5 = CP.PropsSI("H", "T", T_5, "P", P_5, fluid)/1000 #air enthalpy at turbine inlet in kJ/kg
h_6 = CP.PropsSI("H", "D", D_6, "P", P_6, fluid)/1000 #air enthalpy at turbine outlet in kJ/kg
m_air = W_r134a / (h_5 - h_6) #required air flow-rate in kg/s
print('The required air flow-rate to run the compressor is:', f"{m_air:.1f}", 'kg/s')
The required air flow-rate to run the compressor is: 0.6 kg/s