6.12: Second Law for a Refrigration Cycle

6.12: Second Law for a Refrigration Cycle#

Problem Statement#

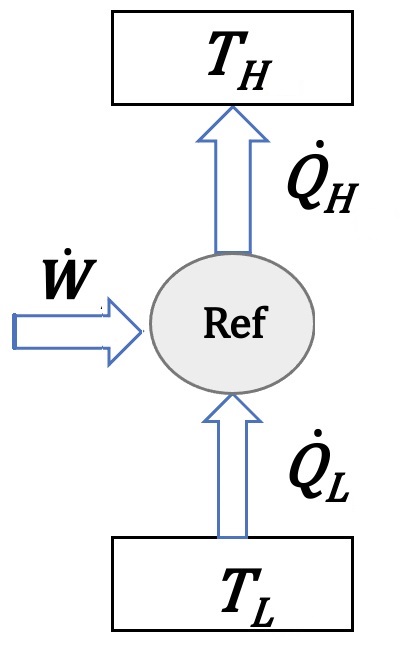
A refrigration cycle works between a cold space at temperature \(T_L\) and a heat sink at a high temperature \(T_H\). Given the cooling load of the cycle is \(\dot Q_L=50\:kW\) and the compressor consumes \(\dot W=10\:kW\) of electric power, calculate:

a) heat dissipated into heat sink

b) COP of the cycle

Assuming the heat absorbtion from the cold environment happens at \(T_L=-20\:^{\circ}C\) and the heat dissipation to the heat sink is at \(T_H=60\:^{\circ}C\), calculate

c) entropy generation (is this feasible?)

d) COP of the Carnot cycle (how does this compare?)

Assuming the cycle operates with a Carnot COP,

e) how much work is required for the same cooling load

f) how much heat is dissipated into the heat sink

g) entropy generation

Solution Approach for a)#

from the first law

\(\dot Q_H=\dot Q_L+\dot W\)

#define inputs
Q_L = 50e+3   #heat absorbed from cool space in W
W = 10e+3   #cycle work input in W
Q_H = Q_L + W   #heat dissipated into heat sink in W

print('The amount of heat dissipated into heat sink is:', f"{Q_H/1000:.1f}", 'kW')

The amount of heat dissipated into heat sink is: 60.0 kW

Solution Approach for b)#

for a refrigration cycle

\(COP=\dot Q_L/\dot W\)

COP = Q_L / W   #COP of the cycle

print('The COP of the cycle is:', f"{COP:.1f}")

The COP of the cycle is: 5.0

Solution Approach for c)#

from the second law for a closed system

\(S_2-S_1=\Sigma Q/T+S_{gen}\)

since the cycle is steady

\(S_2-S_1=0\)

therfore

\(S_{gen}=-\Sigma Q/T=-(Q_L/T_L-Q_H/T_H)\)

#define variables
T_L = -20 + 273.15   #low temperature in K
T_H = 60 + 273.15   #high temperature in K

S_gen = -1 * (Q_L / T_L - Q_H / T_H)   #negative sign for Q_H due to heat leaving the system
print('The entropy generation of the system is:', f"{S_gen:.1f}", 'W/K')

The entropy generation of the system is: -17.4 W/K

Solution Approach for d)#

\(COP_{Carnot,Refrigration}=1/(T_H/T_L-1)\)

COP_C = 1 / (T_H / T_L - 1)

print('The Carnot COP for the cycle is:', f"{COP_C:.1f}")

The Carnot COP for the cycle is: 3.2

Solution Approach for e)#

\(\dot W=\dot Q_L/COP\)

W = Q_L / COP_C

print('The work input for the refrigration cycle based on Carnot operation is:', f"{W/1000:.1f}", 'kW')

The work input for the refrigration cycle based on Carnot operation is: 15.8 kW

Solution Approach for f)#