Ctrl+K

5.7 Refrigeration cycle: Water flow-rate

5.7 Refrigeration cycle: Water flow-rate#

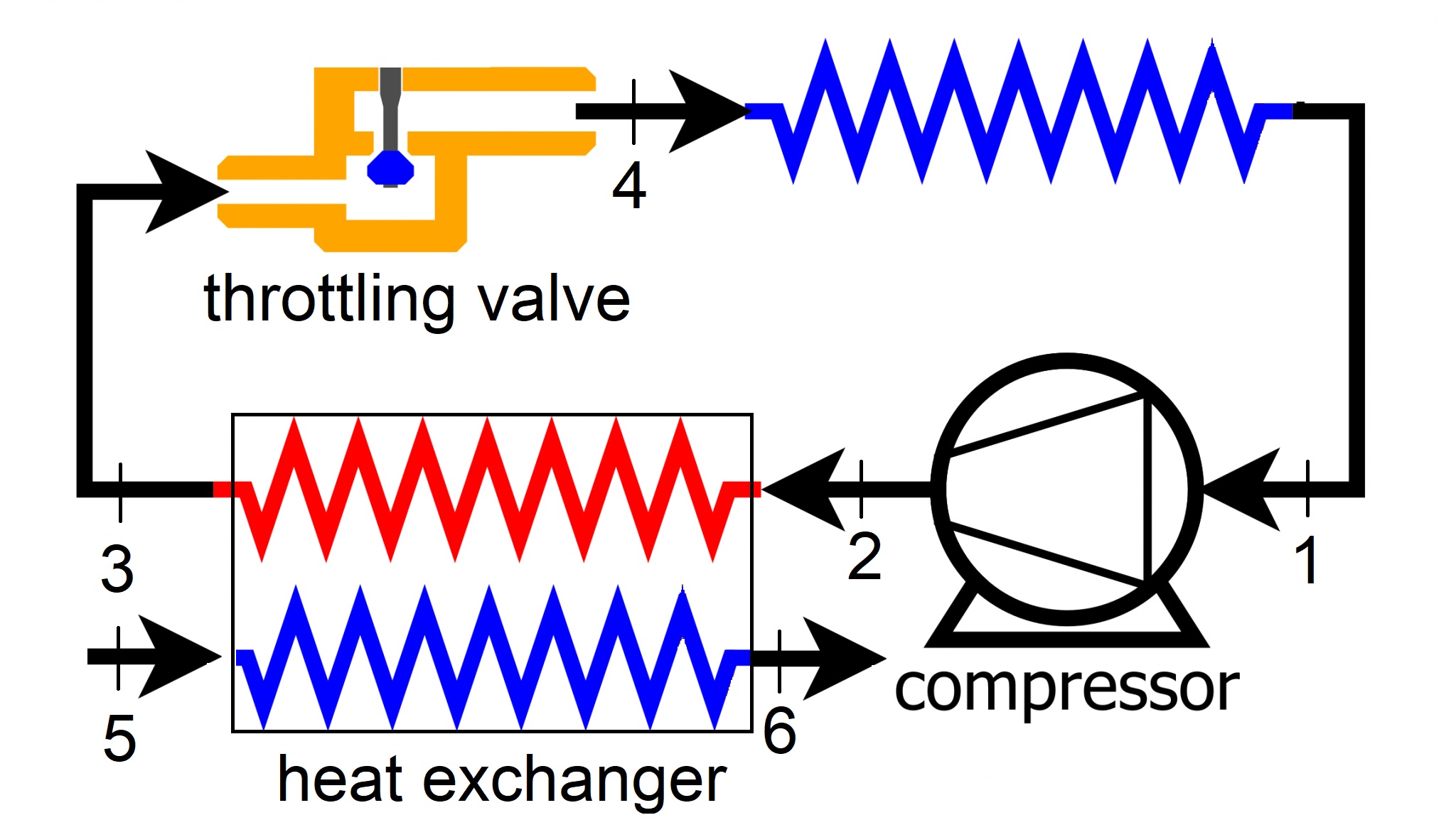
Consider a refrigeration cycle working with R134-a as coolant. The refrigerant absorbs heat at \(-20 ^{\circ} C\) during evaporation and enters the compressor as saturated vapor. The compressor then pressurizes R134-a while the its temperature increases to \(120 ^{\circ} C\). The refrigerant is then cooled down to saturated liquid at \(40 ^{\circ} C\) in constant pressure in a heat exchanger before entering a throttling valve. The refrigerant is then throttled to \(-20 ^{\circ} C\) to provide refrigerating fluid for the evaporator. Assuming the refrigerant exchanges heat with pressurized water in the heat exchanger to heat it up from room temperature to saturated vapor at \(110 ^{\circ} C\), calculate how much water is required per kg of R134a to support cooling power in the heat exhanger.

CH5-Q7.jpg

Solution Approach#

based on the first law of thermodynamics, for the heat exchanger

\(Q+\dot m_ih_i=\dot m_eh_e\)

Assuming an isolated heat exchanger,

\(\dot m_5h_5+\dot m_2h_2=\dot m_3h_3+\dot m_6h_6\)

given

\(\dot m_5=\dot m_6=\dot m_{water}\)

and

\(\dot m_2=\dot m_3=\dot m_{R134a}\)

water flow-rate per \(1\:kg/s\) of \(R134a\) flow-rate would be

\(\dot m_{water}=(h_2-h_3)/(h_6-h_5)\)

from Q#5 of this chapter

## import the libraries we'll need
import CoolProp.CoolProp as CP

# define variables
fluid = "R134A"  # define the fluid or material of interest
T_3 = 40 + 273.15 #stete #3 temperature in K
h_3 = CP.PropsSI("H", "T", T_3, "Q", 0, fluid)/1000  # enthalpy of the refrigerant at state #3 in kJ/kg

h_4 = h_3   #constant enthalpy through a throttling valve

T_4 = -20 + 273.15   #temperature of refrigerant at state #4 in K

P_4 = CP.PropsSI("P", "T", T_4, "Q", 1, fluid)  # pressure of the refrigerant at state #1 in Pa (quality is set to 1 as the pressure keeps constant in sat region)

T_1 = T_4 #temperature at state #1 in K
h_1 = CP.PropsSI("H", "T", T_1, "Q", 1, fluid)/1000  # enthalpy of the refrigerant at state #1 in kJ/kg

T_2 = 120 + 273.15 #temperature at state #2 in K
P_3 = CP.PropsSI("P", "T", T_3, "Q", 0, fluid)  # pressure of the refrigerant at state #3 in Pa
P_2 = P_3 # pressure of the refrigerant at state #2 in Pa
h_2 = CP.PropsSI("H", "T", T_2, "P", P_2, fluid)/1000  # enthalpy of the refrigerant at state #2 in kJ/kg

#for the water side
fluid = "water"
T_6 = 110 + 273.15   #temperature of water at heat exchanger exit in K
T_5 = 25 + 273.15   #temperature of water at heat exchanger inlet in K
h_6 = CP.PropsSI("H", "T", T_6, "Q", 1, fluid)/1000   #enthalpy of water at heat exchanger exit in kJ/kg
P_6 = CP.PropsSI("P", "T", T_6, "Q", 1, fluid)   #pressure of water at heat exchanger exit in Pa
P_5 = P_6   #pressure of water at heat exchanger inlet in Pa assuming constant pressure heating
h_5 = CP.PropsSI("H", "T", T_5, "P", P_5, fluid)/1000   #enthalpy of water at heat exchanger exit in kJ/kg

m_water = (h_2 - h_3) / (h_6 - h_5)

print('The required water flow-rate to support cooling for condensor per kg/s of R134a:', f"{m_water:.1f}", 'kg/s')

The required water flow-rate to support cooling for condensor per kg/s of R134a: 0.1 kg/s
Contents