Ctrl+K

5.3: Air Compressor and Turbine

5.3: Air Compressor and Turbine#

Problem Statement:#

Imagine a turbine whose work output is used to drive a compressor to compress air from atmospheric pressure and temperature to \(1\:MPa\). The turbine operates with steam entering the turbine at \(1.2\:MPa\) and \(600 ^{\circ} C\) and exits as saturated vapor at atmospheric pressure. Assuming air to follow ideal-gas law going through a polytropic process with \(n=1.3\), determine the flow-rate of steam per \(1\:kg/s\) of air flow-rate.

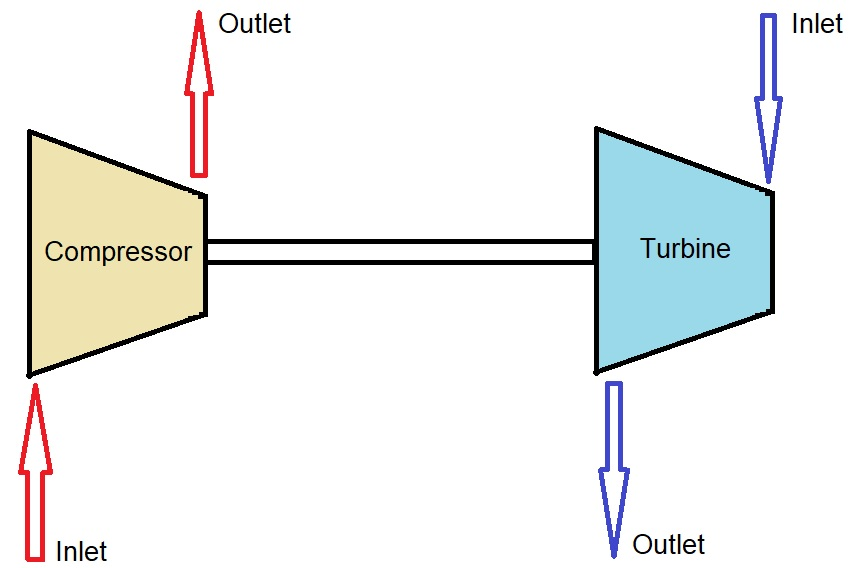
CH5-Q3.jpg

Solution Approach#

Since the turbine and the compressor are coupled, the work output from the turbine is considered the work input for the compressor. Therefore, calculating the work output for unit mass of turbine flow-rate as well as the work input for compressing \(1\:kg\) of air build the bridge to connect the turbine and the compressor and to calculate the required flow-rate.

From the first law of thermodynamics for the turbine assuming no changes in velocity and elevation:

\(w=\Delta h=h_{in}-h_{out}\)

#importing the required library
import CoolProp.CoolProp as CP

#define thermodynamic variables
P_atm = 101325 #atmospheric pressure in Pa
P_it = 1.2E+6 #turbine inlet pressure in Pa 
T_it = 600 + 273.15 #turbine inlet temperatue in K
P_ot = P_atm #turbine outlet pressure in Pa
x_ot = 1#turbine outlet quality

h_it = CP.PropsSI('H', 'P', P_it, 'T', T_it, 'Water') #turbine inlet enthapy J/kg
h_ot = CP.PropsSI('H', 'P', P_ot, 'Q', x_ot, 'Water') #turbine inlet enthapy J/kg

w_t = h_it - h_ot #turbine work output per unit mass of steam in J

For a polytropic process of an ideal gas with a polytropic constant of \(n\):

\(T_2=T_1(P_2/P_1)^{(n-1)/n}\)

for reference look at Example 1 from Chapter 5 in the textbook

n = 1.3 #polytropic constant of the process
T_ic = 25 + 273.15 #inlet temperature of compressor in K
P_ic = P_atm #inlet pressure of compressor in Pa
P_oc = 1E+6 #outlet pressure of compressor in Pa
T_oc = T_ic * (P_oc/P_ic)**((n-1)/n) #outlet temperature of compressor air in K

Now assuming air as an ideal gas, its \(C_p\) value can be used to calculate changes in enthalpy

\(w=\Delta h=h_{out}-h_{in}=C_p(T_{out}-T_{in})\)

#define constants
C_p = 100.5 #Cp of air in J/kg.K
w_c = C_p * (T_oc - T_ic) #specific work input to compress air in J

Now, to correlate mass flow-rates, the rate of work output in the turbine equals to the rate of work input into the compressor

\(\dot W_{turbine}=\dot W_{compressor}\)

\(\dot m_{turbine}w_{turbine}=\dot m_{compressor}w_{compressor}\)

\(\dot m_{turbine}=\dot m_{compressor}w_{compressor}/w_{turbine}\)

m_c = 1 #flow-rate of compressor required in kg/s
m_t = m_c * w_c / w_t
print('The steam mass flow-rate required to compress 1 kg/s of air is',f"{m_t:.3f}",'kg/s')

The steam mass flow-rate required to compress 1 kg/s of air is 0.020 kg/s
Contents