Ctrl+K

6.14 Entropy Generation for a Steam Cycle

6.14 Entropy Generation for a Steam Cycle#

Problem Statement:#

Consider a steam turbine cycle working between a higher pressure \(P_H=1\:MPa\) and a lower presssure of \(P_L=100\:kPa\). The boiler and the condenser are assumed to operate in a constant pressure, and the pump consumes \(\dot W_{pump}=1\:kW\) of electrical power to fulfill the role of pressurizing water from the lower pressure to the higher one. The cycle is designed to operate with a steam flow-rate of \(\dot m=3\:kg/s\) and to provide \(\dot W=12\:kW\) of power from the turbine. \(\dot Q_H=15\:kW\) of heat is provided to the cycle in the boiler section at a temperature of \(T_H=600\:^{\circ}C\), and steam dissipaes heat to the environment in the condenser at an ambient temperature of \(T_L=20\:^{\circ}C\). Calculate:

a) the amount of heat exchanged in the condenser:

b) calculate the efficiency of the cycle

c) entropy generation of the cycle (is this feasible?)

d) calculate the carnot efficicency associated with the higher and lower temperatures and compare with the cycle’s efficiency

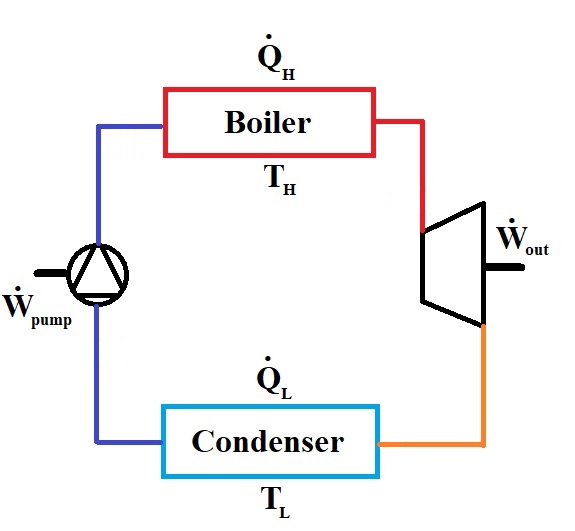
CH6-Q13.jpg

Solution Approach for a)#

Looking at the first law:

\(\dot Q_H+\dot W_{pump}=\dot Q_L+\dot W\)

therefore

\(\dot Q_L=\dot Q_H+\dot W_{pump}-\dot W\)

%%script false --no-raise-error
%colors linux
#define parameters

Q_H =    #heat input in bioler in W
W   =    #turbine work output in W
W_P =    #pump work input in W

Q_L =   #condenser heat in W
print('The amount of heat exchanged in the condenser is:', f"{Q_L/1000:.1f}", 'kW')
Hide code cell source 
#define parameters

Q_H = 15E+3   #heat input in bioler in W
W   = 12E+3   #turbine work output in W
W_P = 1E+3    #pump work input in W

Q_L = Q_H + W_P - W   #condenser heat in W
print('The amount of heat exchanged in the condenser is:', f"{Q_L/1000:.1f}", 'kW')

The amount of heat exchanged in the condenser is: 4.0 kW

Solution Approach for b)#

the efficicency of the cycle would be based on work produced over energy consumed

\(\eta=\dot W/(\dot W_{pump}+\dot Q_H)\)

etha = W / (W_P + Q_H)

print('The efficiency of the cycle is:', f"{etha * 100:.1f}", '%')

The efficiency of the cycle is: 75.0 %

Solution Approach for c)#

from the second law for a closed system

\(S_2-S_1=\Sigma Q/T+S_{gen}\)

since the cycle is steady

\(S_2-S_1=0\)

therfore

\(S_{gen}=-\Sigma Q/T=-(Q_H/T_H-Q_L/T_L)\)

#define variables

T_L = 20 + 273.15   #heat sink temperature in K
T_H = 600 + 273.15   #heat source temperature in K

S_g = - (Q_H / T_H - Q_L / T_L)
print('The amount of entropy generation is:', f"{S_g:.1f}", 'W/K')

The amount of entropy generation is: -3.5 W/K

Solution Approach for d)#

for the carnot efficiency

\(\eta_{Carnot}=1-T_L/T_H\)

etha_c = 1 - T_L / T_H

print('The Carnot efficiency of the cycle is:', f"{etha_c * 100:.1f}", '%')

The Carnot efficiency of the cycle is: 66.4 %
Contents